In the data structures series the next contestant will be the Binary Search Tree. Interestingly in some cases it’s similar to a linked list, and in other cases it’s similar to a graph. Both similarities are correct. In this article I write about these in detail, and I also cover what problem can we have in a BSTree called unbalanced tree.

Basics

Concept

Basically the concept is similar to a linked list, let’s have a node with the content and let’s have neighbor pointers. Here we can have at most 2 neighbors, we call them childs. We can only have maximum two, because this is a binary search tree. This also means that zero or one (left or right) child node is possible. (Quadtree for example can have at most 4 child nodes, hence the name quad.)

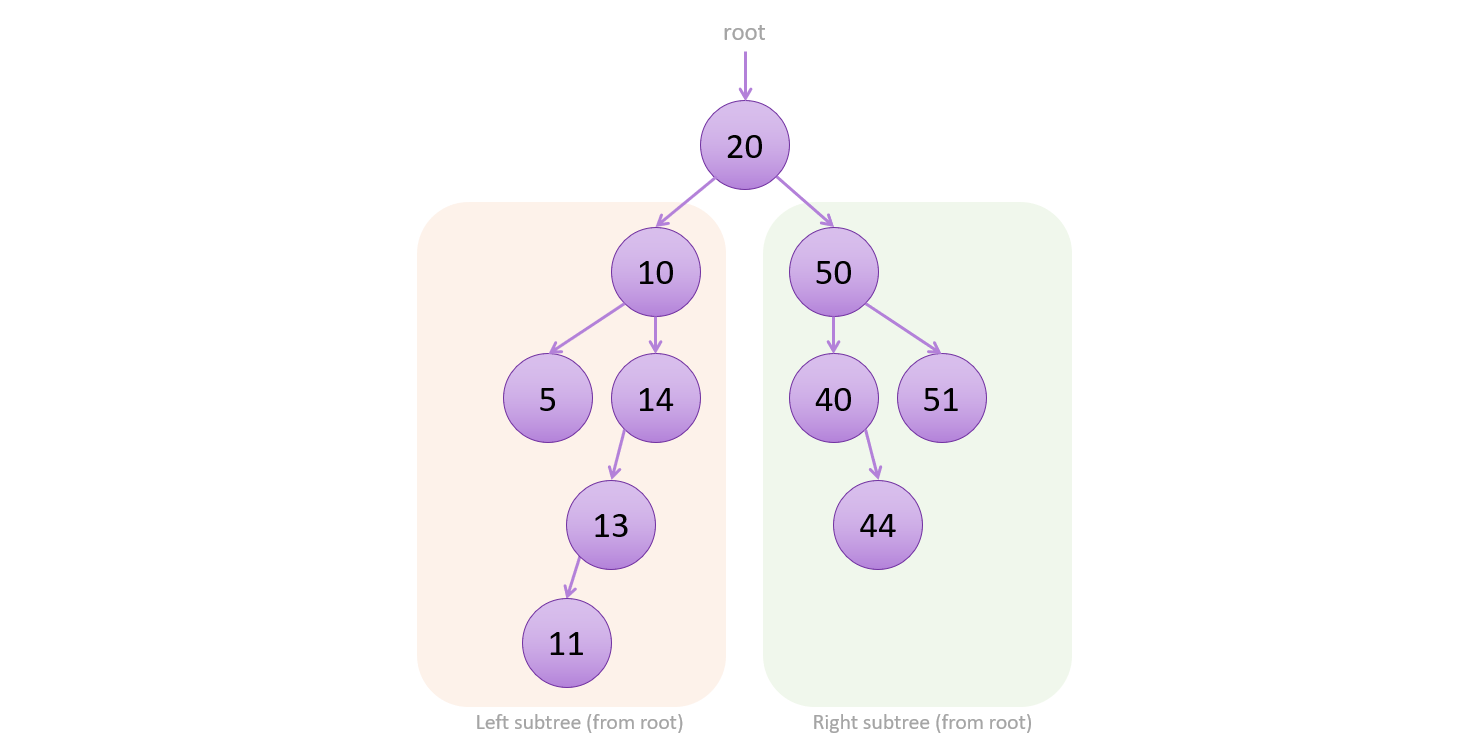
We call it search tree because in an ideal case searching in the structure takes O(log n) time, which is good compared to linked list search time, which was O(n) in general. Ideal case means that the tree is balanced, so the same number of elements are on the left side and the right side. These two sides called left subtree and right subtree. This can be viewed from the root directly, or recursively we can apply the same for each subtree’s subtree let’s say. This image below shows a demonstration binary search tree.

Tree definition

• Tree: the tree is a connected acyclic undirected graph.
• Rooted tree: the tree is a connected acyclic directed graph that satisfies the following properties.
• There exists exactly one node that has no parent (root).
• Each node, except for the root, has exactly one parent.
• The nodes having no children are called the leaves.
• We often draw the rooted tree top-down (the root is at the top and the leaves are down) and sometimes we omit the arrow heads as they always point downwards.
• We sometimes draw the rooted tree bottom-up (the root is at the bottom and the leaves are up) and sometimes we omit the arrow heads as they always point upwards.
• Sometimes we call the tree a tree in broader sense and the rooted tree a tree in narrow sense.

Methods

Traversals

In lists we usually talk about traversal in one way: start from the head and go until reaching the end. However, in BSTrees this is not as easy. Suppose that we start from the root, the questions comes right away: should I step to the left child node, or to the right child node?! After decided, I recursively have to make again a similar decision etc. etc. for each level.

We can have the following traversals, with unique usages:

• PreOrder » save the tree: This traversal type can be good for us if we want to save the tree. After we can re-create the same tree by inserting the same items in the saved order.
• InOrder » sort the items in the tree: Most commonly used traversal, with the help of this we can process the full datastructure in an ordered way. For example if we need to copy the items from the tree to an array in a sorted way, we don’t have to traverse it somehow and then sort the array, we immediately can traverse it in a sorted way.
• PostOrder » free the tree: Also an important traversal type. When you have to delete the full structure you can traverse it like this, and free each node one by one.

Insertion

Insertion is relatively simple, although we have to keep in mind that this is a recursively used datastructure, so we have to adjust our methods accordingly. Compared to a linked list (which can have many forms) the insertion is simple and can be done only one way, there are no special cases. The code below shows, how we can create the two methods for the insertion procedure. Hence the root must not be access from outside, we have to create a public method which then calls the private method starting with the root node.

1
2
3
4
5
6
7
8
9
10
public void Insert(T content, K key)
{ Insert(ref this.root, content, key); }

private void Insert(ref TreeItem p, T content, K key)
{
    if (p == null) p = new TreeItem(content, key);
    else if (p.key.CompareTo(key) < 0) Insert(ref p.right, content, key);
    else if (p.key.CompareTo(key) > 0) Insert(ref p.left, content, key);
    else throw new Exception("Item with the given key already exists.");
}

For more information and detailed code example please see this video below:

Problems

We have to keep in mind that a BSTree is only good for us if it’s balanced. In strange cases the structure can be easily unbalanced, which we try to avoid. Sometimes it can be avoided, but sometimes it can’t. In the second case we can have a logic which rotates us the full tree, remaining ordered. These structured called self-balacing trees, eg. red-black tree or b-tree. Here I don’t talk about it but worth mentioning because unbalanced trees have to be solved somehow.

Red-black tree

The concept here is self-balacing, so when we tree reaches a state when it gets noticeably unbalanced, it rotates itself. This rotation can be seen here.

B-tree

The concept here is a bit different. Instead of correcting itself with rotations, b-trees grow from bottom to top. This means, that the bottom part will always be balanced as you can see here.